current electricity|class12|physics revision notes|part2

current electricity:🔽

 

Cells in Series combination:

Cells are connected in series when they are joined end to end so that the

same amount of electricity  flow through each cell.

when n number of cells identical in nature are joined in series.

then,

 

Total emf of the battery = nE .

Total Internal resistance of the battery = nr

 

Total resistance of the circuit = nr + R

 

Current

 I =nE/nr + R

  note:

  If R << nr, then I = E / r .

If R>>nr, then I = n (E / R).

 

 

Cells in Parallel combination:

 

Cells are said to be connected in parallel,(parallel arrangement is formed ,when cells are joined positive to positive and negative to negative) such that current is divided between the cells. emf remain same in circuit when they are joined in parallel.and it is equal to  a single cell

 The emf of the battery is the same as of a

single cell.

The current in the external circuit is divided equally

among the cells.

 The reciprocal of the total internal resistance is the

sum of the reciprocals of the individual internal

resistances.

now,

 

Total emf of the battery = E

Total Internal resistance of the battery = r / n

Total resistance of the circuit = (r / n) + R

Current I =nE / nR + r

note:

 If R << r/n, then I = n(E / r) 

 If r/n << R, then I = E / R

KIRCHHOFF’S LAWS:

 in simple circuit we use ohms law to calculate current and potential difference,but in complex circuit it is not easy to calculate electric current and potential difference with the help of ohms law to solve this problem ,Kirchhoff  give two laws to calculate current and potential difference in complex circuit

commonly known as 

1.KIRCHHOFF’S I LAWS or junction rule

2.KIRCHHOFF’S I LAWS or voltage law

 

KIRCHHOFF’S I LAWS or Junction Rule:

 

The algebraic sum of electric currents at a junction in any electrical network is always zero.

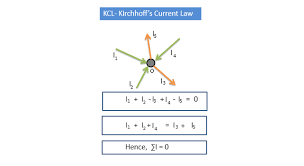
I1 - I2 - I3 + I4 - I5 = 0

 

Sign Conventions:

1. The incoming currents towards the junction are taken positive.

2. The outgoing currents away from the junction are taken negative.

KIRCHHOFF’S LAWS II Law or Voltage Law :

 

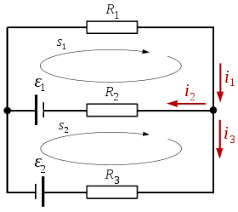
The algebraic sum of all the potential drops and emf’s along any closed path in an electrical network is always zero.

 

 for Loop ABCA:

- E1 + I1.R1 + (I1 + I2).R2 = 0

 

Sign Conventions:

 The potential fall is taken as  negative.

 

The potential rise is taken as  positive.

 

The emf is taken as  negative when we move from positive to negative

terminal of the cell through the electrolyte.

The emf is taken as  positive when we move from negative to positive

terminal of the cell through the electrolyte.

The potential falls along the direction of current in a current path

and it rises along the direction opposite to the current path.

 The path can be moved in any direction  of the loop.

Wheatstone Bridge:

Wheatstone Bridge was originally developed by Charles Wheatstone to measure unknown resistance 

Principle:

"A circuit used  for measuring an unknown resistance by forming a quadrilateral with three known resistances to find a unknown resistance,by reaching a balance condition (when no deflection in the galvanometer)."

For Loop ABDA:

-I1.P - Ig.G + (I - I1).R = 0         ___(i)

Currents through the arms are calculated by applying Kirchhoff’s Junction Rule and Kirchhoff’s Loop Rule 

now,

 

 for Loop BCDB:

- (I1 - Ig).Q + (I - I1 + Ig).S + Ig.G =0.   ____(ii)

 

When Ig = 0, the bridge is said to balanced.,when there is no deflection in galvanometer

now, 

on solving equation (i) and (ii) we have,

 

P/Q=R/S

 

this is  balanced condition of Wheatstone bridge.

Metre Bridge:

 

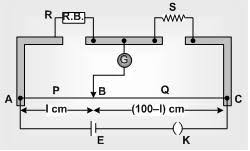
Principle:

Metre Bridge is based on the principle of  Wheatstone Bridge.When the galvanometer current is made zero by adjusting the jockey position on the Metre bridge wire for the given values of known and unknown resistances,

 by using balanced condition of Wheatstone bridge,we have

X /R=100 - l/l

  where X=unknown resistance,and R=Known resistance,l=balancing length.

(Since,Resistance α length)

Therefore,

unknown resistance X is  calculated by knowing known resistance R and balancing length l with the help of given formula,

 

 X = R (100 – l) ⁄ l

Potentiometer:

  Potentiometer used to measure potential difference in a circuit.

Principle:

For a wire having uniform area of cross section and uniform composition,the potential drop across the wire is directly proportional to the length of wire.

V = I R = I ρl/A             ______________(R=ρl/A  )

If the constant current flows through the Potentiometer wire of uniform cross sectional area

 Potential difference is directly proportional to length of the Potentiometer wire

 V α l

V /l =constant.

The potential difference across any length of a wire of uniform cross-section and uniform composition is proportional to its length when a constant current

flows through it

Comparison of emf’s using Potentiometer:

we can compare emfs of different cell using Potentiometer

 

The balance point is obtained for the cell when the potential at a point on the Potentiometer wire is equal and opposite to the emf of the cell.

emf of 1 and 2 cells are given below,

 

E1 = IR1 = I ρ l1 /A ___(i)

E2 =IR2  = I ρ l2 /A ___(ii)

 

On dividing equation (i) and (ii),we have,

 

E1 / E2 = l1 /l2

by knowing balancing length of Potentiometer wire we can compare emf